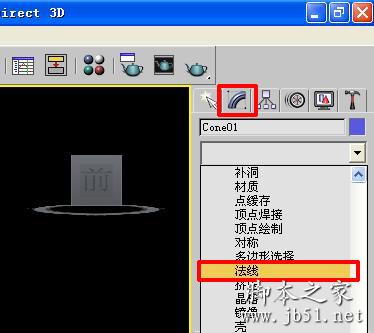
什么是法线?AutoCAD详细解析法线

第一部分

这集说一个重要的东西"法线"。因为我在这上面吃了不少苦头，所以要急着说说，避免初学朋友重走我的弯路。"法线"是什么呢？大家也许都知道,不过还得说说。初中讲几何光学时，光的入射角与反射角相等，而中间这条线就是"法线"；还有是在学习"圆"的时候，过切点并且跟切线垂直的线就叫"法线"。在高中阶段学习直线的的几种形式中，有一种就叫"法线式"，而"法线式"和"一般式"一样是可以适合一切直线的。这些都是平面上的法线，跟cad中的法线说法上不同。

cad中的法线是通常是针对三维来说的，可以简单地理解为垂直于"面"的矢量，在cad中通常不考虑这个矢量的大小，而重点是这个矢量的方向。虽然有人提到cad中的"右手定则"，我觉得这样仍然让初学朋友不太清楚，不知道有什么用处，不容易迅速地运用在实践中。

所以我在另一帖中，根据自己的的认识，借用了电学上的"右手螺旋定则"这个说法。这个"右手螺旋定则"是什么意思呢？如下图所示，就是说如果拇指的指向是法线的正方向，则"角度"的正方向就是四指弯曲的方向。

这个定则细说一下，有：

1、如果知道当前的旋转的正负（cad默认和数学上是一样的，逆时什为正，顺时什为负），就确定的法线的方向。

2、如果知道了法线的方向，可以确定旋转是往哪边进行的，就是方向问题。

3、用两点来指定法线方向时，第一点为掌根，第二点为拇指（切记！！）

初学朋友切不可认为就这么简单结论，有多少值得大吹大擂的？要知道，这里面学问就多了，以后遇到旋转角度之类的问题就可以迎刃而解了。空说无益，结合几个实例，就清清楚楚了。

在实体时旋转，你能完全控制实体的旋转方向吗？这个问题不容易看出来哦，因为我们旋转时，通常是一整周（360度），不管正转还是反转，结果都是一个回转体，看不出旋转方向。但是旋转如30度时，这个问题就必须要考虑了。举例说明之。

在第1、2集中，我就说过这种问题，一定对旋转的过程做到心中有数。

实体编辑中"旋转面"，和"实体旋转"方法是一致的，但是结果的本质却不同，做出的不是回转体。"旋转面"和实体旋转是一样的，当指定一个面后，系统提示指定旋转轴的第一点，这时脑子一定要清晰，这一点就是对应"右手螺旋定则"中的"掌根"；系统提示指定旋转轴的第2点，这一点就是对应"右手螺旋定则"中的"拇指"。比划一下右手，此时四指弯曲的方向就是角度的正方向,这时就可以输入角度了(cad中旋转面为正负90度之间)。

用右手螺旋定则旋转面是相当有用的，因为很多时候，实体较多，面较多时，需要用"三维动态观察器"来查看实体，视点的变化，不容易把握住旋转面的旋转方向，这时比划一下右手，就心中有数了。［这些可是秘密哦，一般人我不告诉他！我也是这样做的哦！不管视点如何变化，这个规律是不变的，比划一下右手，轻松搞定。］

在旋转时，系统提示用两个点来确定旋转轴，再强调一下，指定旋转轴上两个点的先后秩序，第一点为"掌根"，第二点为"拇指"。如果自己指定相反了，也非常好办，想想这个定则，输入相反的角度（如果是30度，就输入-30度）就解决了。

据我观察，右手螺旋定则在cad中是普遍存在的规律，不光用于旋转，在其它地方也是这样的。说句自以为是的话，我当初对于旋转的方向是经常是猜测中进行，在平面上好猜，空间视点一乱则一脸茫然，自从总结出这个规律后，就发现cad不再那样"桀骜难训"。

再次希望初学朋友记住这个规律，避免了一个弯路。

第二部分

"法线"的用途不光是在旋转时的这一种用途。在渲染时，渲染选项中就有"法线为负"的这项，它有什么意义呢，我随便画一图来说明一下，请比较它们的区别！尤其是后面的两种情况，注意贴图后结果的不同。

第三部分

"法线"在cad三维中是个相当重要的概念，但是我观察基本上没人单独详细地讲解它，结果造成相当多的混淆！

比如"剖切"命令中，有个"z轴"的选择项，这是如何运用的呢？我最初毫不迟疑地认为，这是根据当前坐标轴（包括ucs）中z轴的指向来确定剖切面的，因为"剖切"命令中"zx平面"等几个都是类似的用法，我的理解是"z轴"是指，剖切面通过当前坐标轴上的"z轴"，系统要求指定的点就是说不在"z轴"上的一点，因为坐标轴相当于直线，现在直线和不在直线上的一点都确定了，毫无疑问，剖切面就确定了。没有用过"剖切"命令中"z轴"的朋友，你认为这样分析有无道理？而实际上，我这却是大错特错，我不清楚自己错在什么地方了，反正结果和自己预料的不一样，我不断地试验，不断地观察ucs坐标轴中z轴对结果的

说出来真想哭一场，终于有一天，恍然大悟，"剖切"命令中"z轴"与坐标轴中"z轴"没有关系，而是指剖切面上的法线！（欲哭无泪！），我一直被"z轴"这两个字迷惑了！

如何运用，"剖切"命令中"z轴"来剖切实体呢？请看下图。

cad中这个迷惑的"z轴"（真实姓名叫"法线"这家伙），不光在剖切命令出现过哦，感兴趣的朋友自己找找来。"剖切"命令中"z轴"的用法简单地说，系统提示第一点时，是指的是剖切面上的一点，而第二点就是与剖切面垂直且不在剖切面上的一点，这两点就确定了法线，剖切面就是与法线垂直的面，所以这样就知道了剖切面所在。而与当前坐标轴"z轴"的指示没有关系！！

这集就到此，希望初学朋友不再为旋转时，明明感觉往东转，结果往西转，估计这下往东转，结果又猜对了！想信这下就完全心中有数了吧，仔细一想这个规律又是这样浅显易懂，学cad就是这样，经过一番"痛彻心扉"的苦想后，一旦豁然开朗，却发现折磨自己的东西原来也不怎样嘛，自己想到的东西也不咋样嘛。

最后，回答前几集中一些朋友回帖的问题。

1、为什么实体旋转不成功？

答：作为旋转的对象可以是面域，也可以是多段线。这就是说，不是简单画出线就可以了，要么把它做成面域，要么用二维多段线来画成，这里说的多段线是二维多段线，必须是闭合的多段线，所以在用多段线画图时，最后一步输入"c"来结束，确保完全闭合！还有就是如"矩形"和"正多边形"的实质也就是闭合的多段线，所以它们是可以直接旋转或者拉伸成实体。

就是说，闭合的多段线是可以直接旋转或者拉伸成实体的，当然有些情况也不成功（比如多段线自己发生了交叉，这是成不了实体的，这类情况基本上没遇到过，因为多段线是自己画的，自己不可以画一个无法成功的东西出来而要它成功。）

当然把闭合的多段线再转成面域也是可以的（用bo命令或面域命令），一般无此必要。不过用多段线来沿面域的边界描线则有运用，这个估计是软件自己的原因，我曾多次遇到做比较复杂的面域时（轮廓相当复杂），系统出错，难道是这样的轮廓不可能做成实体吗？我索性用多段线描边，最后封闭，然后拉伸或者旋转，就轻松成功了。所以我总结出这样的经验，如果感觉面域做不好时，就用多段线描边，就这样简单。

和曲面上的旋转不一样，实体旋转的对象必须在旋转轴的一侧（！），不能超过旋转轴。

不管用面域还是用多段线来旋转与拉伸，它们必须是平面的图形，相当多的时候，空间相交的直线从一个视图是封闭的，这样连面域都做不出来，显然这是不能旋转与拉伸的。

2、三维五角星的做法。

这个虽然说过了，应该能看明白。第一步是画出平面上的五角星，这里方法是比较多的，一种方法是画个正5边形，然后连接用直线隔一个连接顶点，平面上的五角星就画出来了，然后就用上面这个方法吧，再用多段线描边。

到拉伸成实体，就是确定拉伸的高度，这个自己指定。但是怎样才能拉伸后汇集成一点，而出现尖顶呢？这一步才算有点"技术含量"，就是用捕捉的方式来倾斜角，为了达到这个目的，动用了"偏移命令"，拉伸实体借助平面上的"偏移"命令，未见别人用过，我可是想了许久的哦，灵感的来源就是大家再熟悉不过的"勾股定理"了，通过两直线边就确定了"仰角"（即正切值）。

相信这位朋友应该清楚怎样做的了吧，只要做几个例子就会完全明白了。

3、渲染时怎么一动鼠标渲染效果就没有了？

这个问题陆续说过，因为渲染极其消耗资源，即使一个简单和结果，可能要渲染一两分钟，如果第一步都渲染的话，电脑真的要休克了。还有一点是，我们渲染的目的是为了最后得到效果图，渲染就是为出图用的，所以渲染时要保存为图片。常规方法用：（1）渲染成图片文件；（2）在工具栏中保存为图片；（3）渲染到渲染窗口中支保存：（4）抓图。所以渲染一动鼠标就消失了，这是正常而且相当必要的。如果要渲染,就要重新点渲染。

4、用cad画三维实体有多大的意义？

用cad画三维实体，因为软件的原因，有相当的东西是做不出来的，比如说拿一个"土豆"来，谁能照着完全画出来，可谓高手了。cad画三维实体，通常适合于一些规则的图形，简单地说，能机床能加工出来的东西，都是可以画的。

虽然cad有一定的局限性，但是用cad来学习三维，我认为是再好不过的了，因为这样可以培养三维思维能力，只有思维能力提高了才是最重要的，软件只是一个工具，过分地依赖优良的工具而且是缺少思维，这终究是难也立足的。总体上说,学画三维最好的学习工具就是cad,而cad三维实体的核心就是运用"实体旋转"和"实体拉伸"工具加上布尔运算。

当实体做出来后，后期是"渲染"，渲染的结果也是最吸引人的地方，相当多的人是看到渲染的结果而萌发了学三维也纳实体的想法。在后面几集中，我侧重是说说自己对渲染的粗略认识。在渲染中常有"实体容易，渲染难"的感觉，因为要想调出自己想要的效果是个相当耗时的过程。

拙帖上传以来,谢谢大家的支持。最初写这个系列纯粹偶然，我是想到那里就写到那里，随心所欲，所以有些朋友感觉比较乱。

以上就是AutoCAD法线的详细解析，希望对大家有所帮助！